Schriftliche Rechenverfahren: Was ist der Übertrag?
Version: | Erscheinungsjahr: 2025 |
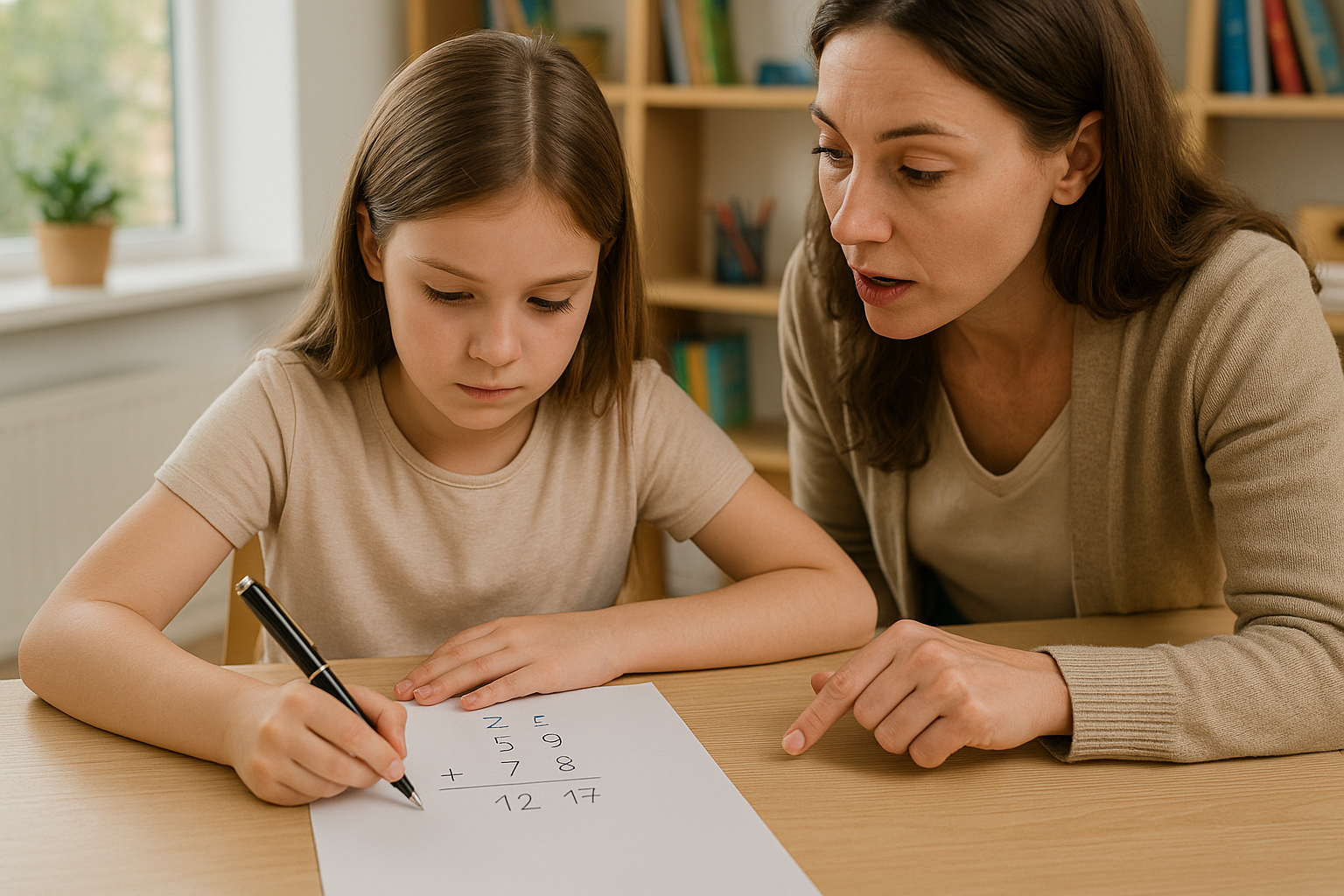
Projektübersicht
- Titel: Schriftliche Rechenverfahren: Was ist der Übertrag?
-
Produktive Webseite: https://moodle.uni-wuppertal.de/mod/hvp/view.php?id=670252#h5pbookid=7529§ion=top&chapter=h5p-interactive-book-chapter-92f005a6-882d-48a8-b349-af42a2305a4b
-
Kategorien: Digitale Bildungsressourcen
-
Technische Anforderungen: Desktop-/Laptop-kompatibel, Headsets und Mikrofone
-
Lernmedien: Aktivierung von Lernenden, Blended Learning, Flipped Classroom (Inverted Classroom), Forschendes Lernen, Gamification , Kollaboratives Lernen, Lernstrategien, Learners as Designers (Lernende als Designer), Lernmedienentwicklung, Projektorientiertes Lehren und Lernen
-
Themen: H5P visualisieren
Kurze Beschreibung:
Verschiedenen schriftliche Rechenverfahren der Addition und Subtraktion mit Fokus auf den Übertrag und das Bündeln
Projektverantwortung: Prof. Dr. Marei Fetzer
Projektbeschreibung
- Projektziele: Verschiedenen schriftliche Rechenverfahren der Addition und Subtraktion mit Fokus auf den Übertrag und das Bündeln, um Schwierigkeiten auf diesem Gebiet zu erkennen
- Grundlagen des Übertrags und Bündelns: Hier wird ein erster Zugang zu den Konzepten geschaffen, indem das Prinzip des Übertrags verständlich eingeführt wird.
- Darstellung von Zahlen im Stellenwertsystem: In diesem Abschnitt geht es um verschiedene Darstellungsformen von Zahlen, um das Verständnis für flexible Zahlendarstellungen zu fördern.
- Das Sechser-System als alternative Zahldarstellung: Dieser Abschnitt löst sich bewusst von der Konvention des Dezimalsystems. Durch die Auseinandersetzung mit einem alternativen Zahlensystem versetzen sich die Studierenden in die Situation von Kindern, die ein neues Zahlsystem erlernen. Zudem sensibilisieren wir für alternative Darstellungsformen und knüpfen an anfängliche, potenziell fehleranfällige Zählvorgänge an – etwa die Vorstellung, dass nach der 10 nicht „einszehn“ folgt.
- Verschiedene Darstellungsweisen von Stellenwerten kennenlernen und verstehen, dass es nicht nur eine mögliche Lösung gibt.
- Die Erkenntnis, dass nicht gebündelte Ergebnisse nicht per se falsch sind (wie im Anfangsbeispiel), sondern lediglich nicht der standardisierten Schreibweise entsprechen.
- Die Lösungen der Schüler*innen verstehen, ihren aktuellen Lernstand diagnostizieren und sie individuell fördern können.
Lange Beschreibung:
Fachdidaktischer Kommentar zu „Schriftliche Rechenverfahren: Was ist der Übertrag?“
Von Anna Amblank, Lisa Ronsdorf und Sarah Weber
Eine Schülerin zeigt ihrer Lehrerin die Lösung einer schriftlichen Additionsaufgabe und sagt: „Das Ergebnis ist 17 Einer und 12 Zehner.“
Die Lehrerin sieht die Lösung im Heft und antwortet: „Ohje, was hast du denn gemacht? Da musst du aber noch kräftig üben! Das ist Stoff der dritten Klasse.“
Hoffentlich denken Sie sich nach diesem kurzen Dialogausschnitt, dass Sie nicht so defizitorientiert wie die Lehrkraft reagiert hätten. Um Ihnen noch mehr fachliche und didaktische Sicherheit zu geben, soll unsere digitale Lernumgebung helfen. Hätte die Lehrkraft unsere Lernumgebung durchlaufen, hätte sie verstanden, dass die Schülerlösung „17 Einer und 12 Zehner“ nicht falsch ist. Zudem hätte sie das Prinzip des Bündelns in der Tiefe verstanden und gewusst, dass es mehrere korrekte Zahldarstellungen gibt. Darüber hinaus hätte sie sich mit dem Sechser-System auseinandergesetzt, was ihr geholfen hätte, sich besser in das Kind hineinzuversetzen und zu verstehen, was es bedeutet, ein neues Zahlsystem zu erlernen.
Im Rahmen des Moduls GMG 10 haben wir uns intensiv mit den verschiedenen schriftlichen Rechenverfahren der Addition und Subtraktion beschäftigt. In unserer Lernumgebung haben wir den Fokus auf den Übertrag und das Bündeln gelegt, da in diesen Bereichen häufig Schwierigkeiten auftreten.
Unsere Lernumgebung ist in drei zentrale Teile gegliedert:
Zielgruppe: Die Zielgruppe dieser Lernumgebung sind Lehramtsstudierende für das Grundschullehramt aller Semester.
Lernziele: Mit unserer Lernumgebung möchten wir folgende drei Hauptziele bei den Studierenden erreichen:
Durch die vertiefte Auseinandersetzung mit diesen Themen hoffen wir, Lehramtsstudierende auf die Herausforderungen des Mathematikunterrichts in der Grundschule vorzubereiten und ihnen das notwendige didaktische Wissen zu vermitteln, um Kinder bestmöglich zu begleiten.

